Bienvenue à la page Géométrie de MathsLibres.com ou il n'y a rien de mal à être plat. Sortez vos règles, vos compacts et vos rapporteurs d'angles et préparez-vous pour des fiches d'exercices splendides traitant la Géométrie des angles et des coordonnées, les triangles, les quadrilatères, les transformations, les constructions et la Géométrie 3-D!
Les quadrilatères de la section ressources sont tout prêts à être découpés, mesurés, pliés, comparés, et anotés. Elles peuvent être très utiles lors de l'instruction des concepts de géométrie reliés aux quadrilatères. Juste après l'ensemble de quadrilatères, vous allez trouver des feuilles de travail sur la géométrie des angles. Vous pouvez aussi voir aussi la page « Mesure » pour plus d'exercices sur les angles.
La majorité de cette page est dédiée aux transformations. Les transformations géométriques présentent un sujet que les élèves trouvent souvent très intéressant. Nous avons donc créé assez de feuilles de travail pour les garder bien occupés. Ne manquez surtout pas le monde intéressant et stimulant des constructions de cubes qui se trouve au bas de la page. Il se peut que vous repéreriez quelques futures artistes lorsque vous ferez utiliser ces fiches dans vos classes.
Fiches d'Exercices sur la Géométrie le Plus Populaires cette Semaine

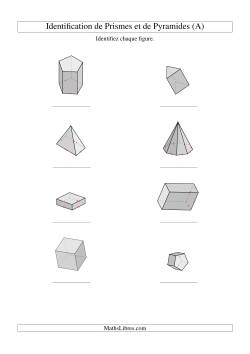
Ressources
Cette rubrique des ressources comprennent les tangrams, ensembles de formes et diverses lignes.
Ensemble de formes
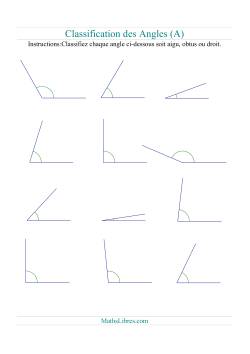
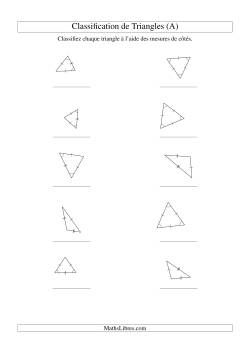
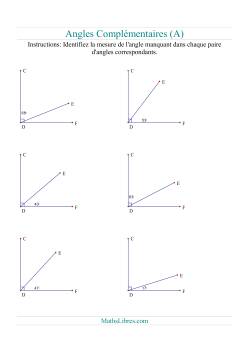
Géométrie des Angles
Que serait une page sur la Géométrie sans la présence de fiches d'exercices sur les angles? Les fiches de cette sections ne contienne que des exercices sur la classification des angles et de leurs relations. Veuillez bien passer à la page « Mesure » pour trouver des exercices sur la mesure des angles.
Relations entre angles
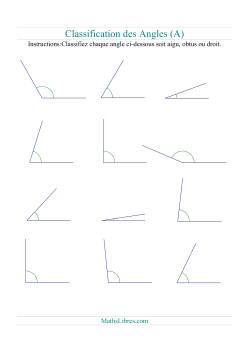
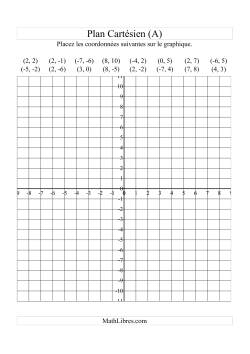
Géométrie des Points de Coordonnées
Le but de cette section est d'aider les élèves à mettre le « point » sur leur étude du plan Cartésien. Nous avons cré quelques feuilles de travail uniques qui appuyeront vos élèves sur leur chemin.
Placement de points dans un repère
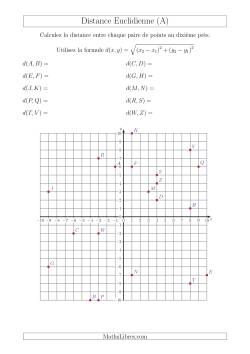
Distance Euclidienne & Périmètre et Aire des Polygones
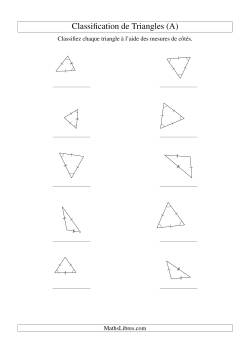
Triangles
Des fiches d'exercices contenant la classification des triangles selon leur côtés et les propriétés d'un angle.
Classification de triangles
Cercles
Les fiches d'exercices sur les Cercles pour vous aider à calculer les mesures de cercles: rayon, diamètre, circonférence et aire.
Calculs de Circonférence, Rayon, Diamètre et Aire d'un Cercle

Le rayon, la diamètre, la circonférence et l'aire sont toutes les mesures connexes; vous avez seulement besoin de l'un d'eux pour trouver les mesures restantes. Le diamètre et le rayon sont les plus simple parce que le diamètre d'un cercle est deux fois le rayon et, inversement, le rayon est la moitié du diamètre. Pour calculer entre rayon/diamètre et circonférence/aire, vous devez utiliser π (pi). Selon votre accessibilité aux calculatrices ou ordinateurs, vous pouvez utiliser plusieurs décimales de pi dans le calcul ou quelques-unes. Souvent, les gens sans calculatrices utilisent une estimation de pi (3 ou 3.14). Le calcul sur les fiches d'exercices ci-dessous utilise une version assez précise de pi; vous pouvez si vous le désirez, ajuster les réponses si vous utilisez des versions plus arrondies de pi.
Quadrilatères
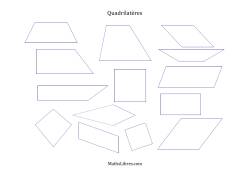
Des fiches d'exercices contenant la classification de quadrilatères.
Classification de quadrilatères

Transformations
Fiches d'exercices sur les transformations pour pratiquer les translations, les réflexions, les rotations et les homothéties.
Voici deux méthodes de vérification simples et effectifs que vous pouvez utiliser lorsque vous corrigez les fiches ci-dessous. Pour commencer, vous pouvez superposer la copie de votre élève sur la feuille réponse et les placer devant un lumière. De lÀ, vous n'avez qu'À glisser les pages un tout petit peu pour déduire si les réponses sont correctes. Gardez la copie de votre élève sur le dessus pour pouvoir facilement ajouter vos corrections et commentaires. La deuxième méthode nécessite que vous imprimez la fiche de solutions sur une acétate. Surperposez le transparent sur la copie de votre élève, et soulevez-le au fur et à mesure que vous voulez ajouter vos corrections.
Translations à une étape
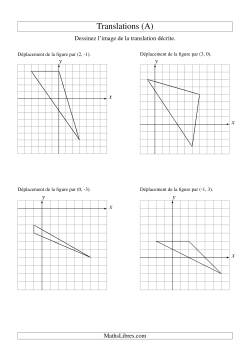
Translations à deux étapes
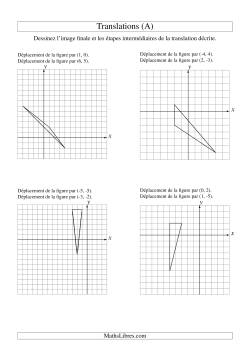
Translations à trois étapes
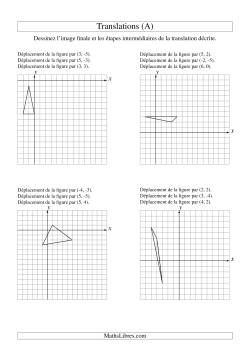
Réfléchissez sur ceci: la réflexion des formes géométriques par rapport aux axes horizontaux ou verticaux est assez simple, surtout si vous effectuez la réflection dans une grille de coordonnées. Partez d'un des sommets de la figure et mesurez ainsi la distance de ce sommet à l'axe de réflexion. Notez bien que votre ligne de mesure doit être perpendiculaire à (À 90 degrés de) l'axe de réflexion, ce qui est en fait la raison pour laquelle la réflexion par rapport aux lignes horizontales et verticales est généralement plus facile. Remesurez ensuite la même distance (encore à 90 degrés de l'autre côté de l'axe de réflexion et inscrivez un point pour marker la position du sommet réfléchi. Lorsque vous aurez complétez les étapes ci-dessus pour chancun des sommets de la figure, vous n'aurez qu'À relier les sommets adjacents de la nouvelle figure à l'aide de segments de droite et voilÀ!.
Effectuer une réflexion peut être aussi simple que plier un feuille de papier. Pliez la feuille au long de la droite de réflexion et placez-la devant la lumière. Le jour, une fenêtre s'avère à être un bon choix de source de lumière car vous aurez ainsi aussi un surface sur laquelle vous pourrez dessiner. N'essayez pas de dessiner la figure en entière lorsqu'elle est placée sur la fenêtre. Tracez plutôt les points des sommets et replacez, ensuite, la feuille sur votre table ou burreau. Par la suite, dépliez la feuille et utilisez une règle pour rattacher les sommets avec les segments de la figure.
Réflexions à une étape
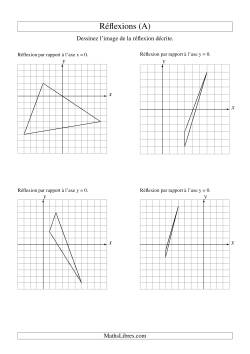
Réflexions à deux étapes
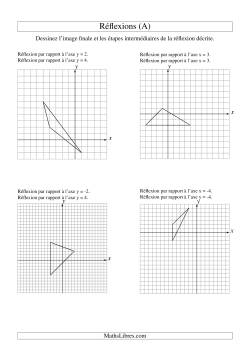
Réflexions à trois étapes
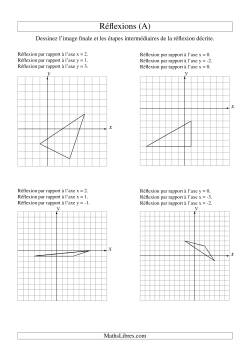
Voici une idée qui vous permettera d'effectuer des rotations sans rien avoir à mesurer. Cette méthode fonctionne le mieux lorsqu'elle est utilisée pour effectuer des rotations dans un plan avec axes de coordonnées. Vous aurez besoin d'une acétate ou d'une autre feuille de plastique transaparente sur laquelle vous pouvez dessiner, et d'une stylo feutre qui laissera des traces sur votre transparent. Nous vous recommendons d'utiliser un stylo feutre non-permanent, car cela vous permettra laver et réutiliser votre feuille de plastique. Commencer par placer la feuille transparente au-dessus de la fiche contenant les axes de coordonnées et la figure de rotation. Avec le stylo, en étant le plus précis que possible, tracez une petite croix sur l'acétate pour marquer les axes de x et y. Tracez aussi les sommets de la figure à être tournée. Utilisez ensuite la feuille de plastique pour effectuer la rotation en réalignant la croix avec les axes. Choississez par la suite un sommet. Tout en tenant bien attention de le garder en place, soulever l'acétate juste assez pour pouvoir marquer la position de ce sommet sur la fiche d'exercice. Procédez ainsi avec les autres sommets de la figures, et soulever ensuite le transparent au complet pour joindre les sommets de la figure sur la fiche à l'aide d'une règle et de segments de droite.
Rotations à une étape
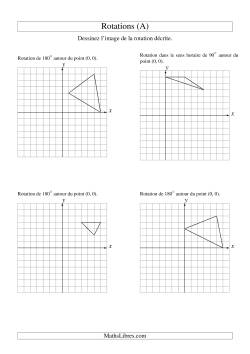
Rotations à deux étapes
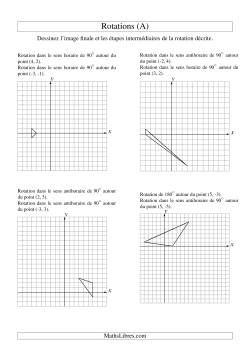
Rotations à trois étapes
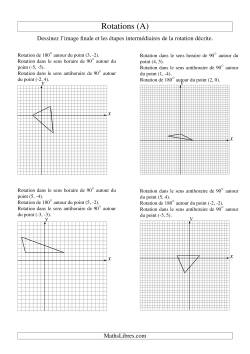
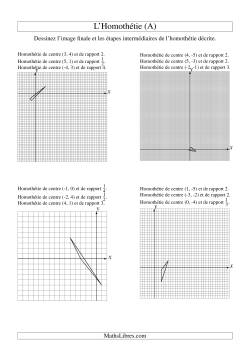
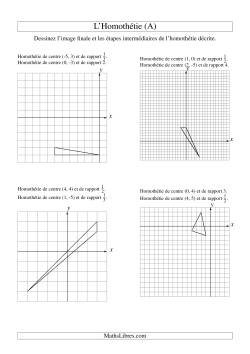
Homothéties à une étape
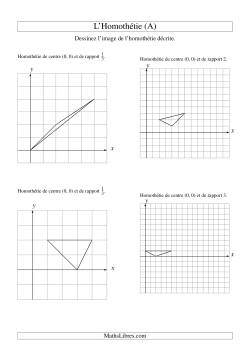
Homothéties à deux étapes
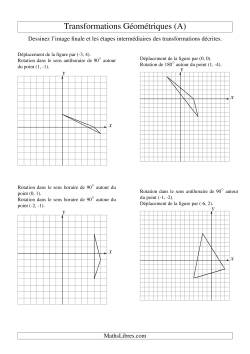
Transformations mixtes incluant les translations, les réflexions, les rotations et les homothéties
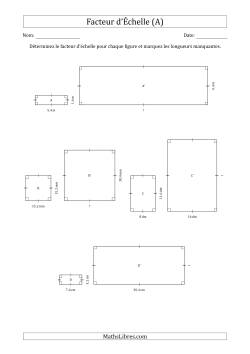
Facteur d'Échelle
Constructions
C'est incroyable ce qu'on peut accomplir avec une compas, une arête droite et un crayon. Dans cette section, les étudiants feront les maths comme Euclide l'a fait il y a plus de 2000 ans. Non seulement cela sera une leçon d'histoire, mais les étudiants acquerront des compétences précieuses qu'ils peuvent utiliser dans les études mathématiques plus tard.
Bissectrices d'un angle

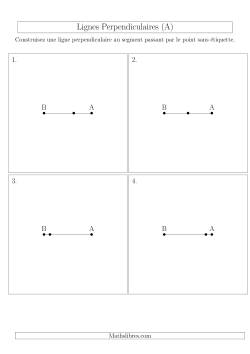
Lignes perpendiculaires
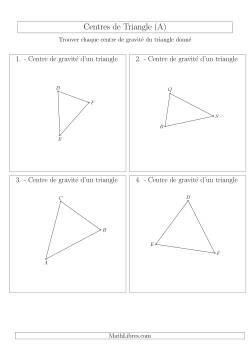
Centres de gravité d'un triangle
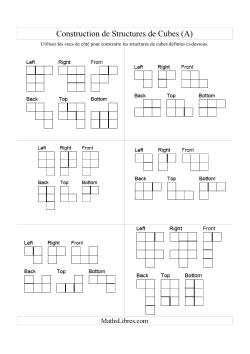
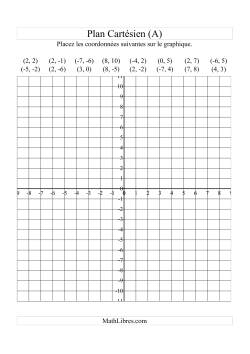
Géométrie Trois-Dimensionnelle
Les constructions de cubes présentent un puissant outil pour le développement du sens spatial de vos élèves. Les deux premières fiches d'exercices ci-dessous peuvent s'avérer un défi en autant pour les jeunes élèves que pour les adultes, mais avec un peu de pratique, vos élèves réussiront à créer des structures beaucoup plus complexe que ceux que vous trouverez ci-dessous. L'utilisation du papier isométrique, quadrillé ou pointé facilitera la tâche de dessin des croquis trois-dimensions ou des vues de côtés de structures de cubes existantes. Vous trouverez une panoplie de feuilles de papier isométriques, quadrillés et pointés sur la page « Papier Graphique » de notre site.
Développement des Solides de Platon et d'Archimède
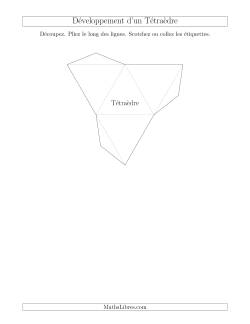
Pour construire un objet de l’espace il faut dessiner ce qu’on appelle son développement (ou patron) qu’il suffira alors de découper et de plier pour former le solide. Une paire de ciseaux, un petit ruban et une dextérité sont tout ce dont vous avez besoin. Pour quelque chose d’un peu plus substantiel, copier ou imprimer d’abord les développements sur un papier cartonné. Vous pouvez également vérifier vos paramètres d’impression pour s’assurer que vous imprimez dans la « taille réelle » plutôt que de l’ajustage de précision à la page, donc il n’y a aucune distorsion.
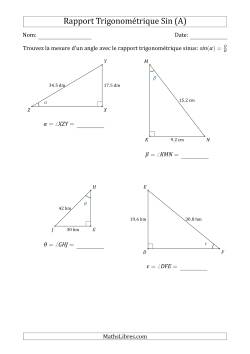
Les Rapports Trigonométriques (Sin, Cos, Tan)
Les rapports trigonométriques ont pour objectifs de se familiariser avec les rapports trigonométriques et de rechercher des mesures manquantes dans les triangles rectangles à l'aide des rapports trigonométriques. Ci-après est un truc pour bien identifier les rapports trigonométriques de base avec sinus, cosinus et tangente. Il suffit de se souvenir de l'expression SOH - CAH - TOA.
- SOH : Sinus = Opposé / Hypothénuse
- CAH : Cosinus = Adjacent / Hypothénuse
- TOA : Tangente = Opposé / Adjacent
Les Rapports Trigonométriques