Bienvenue à la page sur les fractions de mathslibres.com où le verre est à moitié plein! Cette page est l'une de nos plus populaires, sans doute parce que l'apprentissage des fractions est extrêment important dans la vie de quelqu'un et que c'est un sujet que beaucoup appréhendent à cause de sa mauvaise réputation. En réalité, les fractions ne sont vraiment pas si difficiles que ça à maîtriser, surtout avec notre grande variété de fiches d'exercices comme support.
Vous trouverez ci-dessous des centaines de fiches d'exercices sur les fractions. Celles-ci incluent la représentation des fractions, la comparaison, la classification en ordre, la simplification et la conversion des fractions ainsi que les calculs de base avec des fractions. Nous avons commencé par le plus évident: la représentation des fractions. Comme il est important que l'élève comprenne bien le concept d'une fraction, passez un bon bout de temps d'instruction avec des modèles de fraction visuels. Il est plus facile pour l'élève d'assimiler le concept d'une moitié de biscuit que celui d'une moitié de carré alors assurez-vous d'utiliser des exemples concrets le plus souvent possible. Demandez à un élève qu'est-ce qu'on obtient lorsqu'on ajoute une moitié de biscuit à une autre moitié de biscuit, et il vous répondra sans doute qu'on obtient une collation délicieuse.
Le reste des fiches sont vouées à aider les élèves à comprendre le concept des franctions. De la comparaison à la simplification et la conversion ... le temps que vos élèves terminent et maîtrisent le contenu de cette page, les fractions n'auront plus le moindre secret pour eux.
Fiches de Fractions le Plus Populaires cette Semaine




Ressources imprimables générales sur les fractions
Cercles de fractions
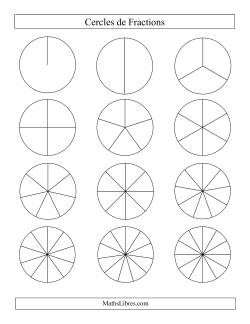
Les cercles de fractions en noir et blanc peuvent être utilisés comme un moyen de manipulation pour comparer les fractions. Photocopiez la feuille de travail sur une diapositive de rétroprojection. Utilisez un crayon pour colorer légèrement le cercle approprié afin de représenter la première fraction sur la copie papier. Utilisez un stylo non permanent pour colorier le cercle approprié pour représenter la deuxième fraction. Posez la diapositive sur le papier et comparez les deux cercles. Vous devriez facilement pouvoir dire lequel est le plus grand ou le plus petit ou si les deux fractions sont égales. Réutilisez les deux feuilles en effaçant le crayon et en lavant le marqueur.
Bandes de fractions

Les bandes de fractions peuvent être laminées pour plus de durabilité et découpées pour comparer, ordonner, ajouter et soustraire des fractions. Elles sont très utiles pour comparer les fractions. Vous pouvez également copier les bandes de fractions sur des transparents de rétroprojection et les découper. Non seulement elles seront durables, mais elles seront également transparentes, ce qui est utile lorsqu'elles sont utilisées avec des versions papier (par exemple pour comparer des fractions).
Fiches d'exercices de représentation des fractions
Vous pouvez essayer d'autres façons intéressantes de représenter les fractions en plus des fiches ci-dessous. Des collations santé peuvent servir de très bon modèle de représentation. Pouvez-vous couper un concombre en tiers? Une tomate en quarts? Peuvent-ils faire en sorte que les deux tiers de leurs raisons soient verts, tandis que le tier restant soit rouges?
Modélisation de fractions avec des groupes de formes
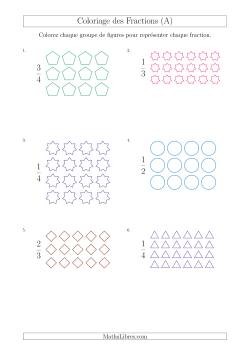
Les fractions peuvent représenter une part d'un groupe ou un part d'un tout. Dans ces fiches-ci, les fractions sont représentées comme étant part d'un groupe.
Modélisation de fractions avec des rectangles
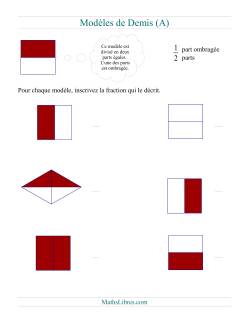
Modélisation de fractions avec des cercles

Fiches d'exercices sur les rapports & les proportions
Images de ratios
Veuillez noter que les feuilles de calcul du ratio des images ci-dessous sont volumineuses et peuvent prendre du temps à charger si vous êtes sur une connexion plus lente.
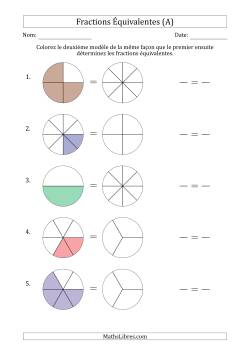
Fractions équivalentes

Les feuilles de travail des modèles de fractions équivalentes ne comprennent que les "fractions de cuisson" dans les versions A. Pour voir des fractions plus difficiles et plus variées, veuillez choisir les versions B à J après avoir chargé la version A.
Ratios équivalents

Fiches d'exercices de comparaisons et de classification en ordre de fractions
Comparaison de fractions simples

Il existe de nombreuses stratégies différentes autres que le simple fait de regarder la page qui vous aideront à comparer les fractions. Essayez de commencer par quelque chose de visuel qui dépeindra les fractions en question. Nous vous recommandons vivement nos bandes de fractions (faites défiler un peu vers le haut). L'utilisation d'une règle, d'un livre ou d'un pliage aidera les élèves à voir facilement quelle fraction est la plus grande ou si elles sont égales. Nous devons également mentionner que les choses qui sont comparées doivent être les mêmes. Chaque bande de fraction par exemple a la même taille alors que si vous preniez un tiers de pastèque et la moitié d'un raisin, la comparaison serait moins claire.
Comparaisons de fractions simples et impropres

Il est aussi possible d'utiliser des repères comme 0, 1, 1/2 pour déterminer où chacune des fractions se positionne sur une droite numérique, afin de voir laquelle est la plus grande. Les élèves utilisent d'ailleurs cette méthode très souvent puisqu'ils peuvent souvent comparer des fractions en reconnaissant qu'une est moins d'une moitié alors que l'autre est plus d'une moitié. Ils peuvent aussi voir que l'une des fractions est nettement plus proche d'un nombre entier que l'autre, même si les deux fractions sont supérieures à une moitié.
Comparaison de fractions simples, impropres & mixtes

Une autre stratégie de comparaison des fractions consiste à convertir chaque fraction en une décimale et à comparer les décimales. Les conversions décimales peuvent être mémorisées (en particulier pour les fractions communes) calculées avec une division longue ou à l'aide d'une calculatrice ou d'une grille de référence. Nous suggérons cette dernière solution, car l'utilisation d'une grille de référence conduit souvent à une mémorisation mentale.
Ordonner des fractions sur une droite numérique

La plupart des stratégies qui fonctionnent pour comparer les fractions fonctionnent également pour ordonner les fractions. En utilisant des outils de manipulation tels que les bandes de fractions, les droites numériques ou la recherche d'équivalents décimaux, vos élèves mettront les fractions dans le bon ordre en un rien de temps. Nous l'avons probablement déjà dit, mais assurez-vous de souligner que lorsque vous comparez ou ordonnez des fractions, les élèves comprennent que le tout doit être identique. Comparer la moitié de la population du Canada avec un tiers de la population des États-Unis ne suffira pas. Essayez d'utiliser quelques éléments visuels pour renforcer ce concept important. Même si nous avons inclus des droites numériques ci-dessous, n'hésitez pas à utiliser vos propres stratégies.
Ordonner des fractions

Les feuilles de travail sur l'ordre des fractions dans cette section ne comportent pas de droite numérique, pour permettre aux élèves d'utiliser diverses stratégies de tri.
Fiches d'exercices de simplification et de conversion de fractions
Arrondir des fractions

Arrondir les fractions aide les élèves à comprendre les fractions un petit peu mieux et est une technique qui peut être utilisée pour estimer les réponses à des questions de fractions. Par exemple, si on essaiyait d'estimer 1 4/7 x 6, on pourrait dire que la réponse est environ 9 puisque 1 4/7 est environ 1 1/2 et que 1 1/2 x 6 fait 9.
Simplification de fractions

Apprendre à simplifier les fractions rend la vie d'un étudiant beaucoup plus facile par la suite lorsqu'il apprend des opérations avec des fractions. Cela les aide également à apprendre que des fractions d'apparence différente peuvent être équivalentes. Une façon de le démontrer est de diviser deux fractions équivalentes. Par exemple, 3/2 et 6/4 donnent tous deux un quotient de 1,5 lorsqu'on les divise. En s'exerçant à simplifier les fractions, les élèves pourront, espérons-le, reconnaître les fractions non simplifiées lorsqu'ils commencent à additionner, soustraire, multiplier et diviser avec des fractions.
Conversion entre fractions impropres et fractions mixtes

Conversion entre des fractions, des nombres décimaux, de pourcentages et des ratios

Fiches d'exercices d'opérations avec des fractions
Multiplication de fractions

La multiplication des fractions est généralement moins déroutante sur le plan opérationnel que toute autre opération et peut être moins déroutante sur le plan conceptuel si elle est abordée de la bonne manière. L'algorithme de multiplication consiste simplement à multiplier les numérateurs puis à multiplier les dénominateurs. Le mot magique pour comprendre la multiplication des fractions est "de". Par exemple, qu'est-ce que deux tiers DE six ? Qu'est-ce qu'un tiers DE la moitié ? Lorsque vous utilisez le mot " de ", il devient beaucoup plus facile de visualiser la multiplication des fractions. Exemple : coupez un pain en deux, puis coupez la moitié en tiers. Un tiers d'une moitié de pain équivaut à 1/3 x 1/2 et a un goût délicieux avec du beurre.
Division de fractions

Conceptuellement, la division des fractions est probablement la plus difficile de toutes les opérations, mais nous allons vous aider. L'algorithme de division des fractions est identique à celui de la multiplication des fractions, mais vous trouvez l'inverse de la deuxième fraction ou vous effectuez une multiplication croisée. Cela vous permet d'obtenir la bonne réponse, ce qui est extrêmement important, surtout si vous construisez un pont. Nous vous avons dit comment conceptualiser la multiplication des fractions, mais comment cela fonctionne-t-il avec la division ? Facile ! Il vous suffit d'apprendre la phrase magique : «Combien de fois __ entre-t-il dans __?» Par exemple, dans la question 6 ÷ 1/2, on se demanderait, «Combien de moitiés entrent dans 6?». Cela devient un peu plus compliqué lorsque les deux nombres sont des fraction, mais ce n'est guère impossible. 1/2 ÷ 1/4 en est un exemple relativement facile, surtout si vous pensez en termes de pièces de dollars US ou canadien. Combien de pièce de 25 sous y a-t-il dans la moitié d'un dollar?
Addition de fractions

L'addition de fractions nécessite le fâcheux dénominateur commun. Facilitez la tâche à vos élèves en leur enseignant d'abord les concepts de fractions équivalentes et de plus petits multiples communs. Une fois que les élèves se sont familiarisés avec ces deux concepts, l'idée de trouver des fractions avec des dénominateurs communs pour l'addition devient d'autant plus facile. Passer du temps sur la modélisation des fractions aidera également les étudiants à comprendre l'addition des fractions. Relier les fractions à des exemples familiers sera certainement utile. Par exemple, si vous ajoutez une 1/2 banane et une 1/2 banane, vous obtenez une banane entière. Que se passe-t-il si vous ajoutez une 1/2 banane et 3/4 d'une autre banane?
Fiches d'exercices sur l'addition de fractions mixtes

Une stratégie courante à utiliser lors de l'ajout de fractions mixtes est de convertir les fractions mixtes en fractions impropres, de compléter cette opération, puis de revenir en arrière. Une autre stratégie qui demande un peu moins de réflexion consiste à examiner les nombres entiers et les fractions séparément. Ajoutez d'abord les nombres entiers. Ajoutez ensuite les fractions. Si la fraction résultante est impropre, il faut la convertir en un nombre mixte. La portion de nombres entiers peut être ajoutée à la portion de nombres entiers d'origine.
Soustraction de fractions

Il n'y a pas beaucoup de différence entre l'addition et la soustraction de fractions. Les deux requièrent un dénominateur commun, ce qui exige certaines connaissances préalables. La seule différence est que le deuxième numérateur et les numérateurs suivants sont soustraits au premier. Il y a un risque de se retrouver avec un nombre négatif lors de la soustraction de fractions, et les étudiants doivent donc apprendre ce que cela signifie dans ce cas. Lorsqu'il s'agit de n'importe quel concept relatif aux fractions, il est toujours bon de le relier à une situation familière ou facile à comprendre. Par exemple, on peut donner une signification à 7/8 - 3/4 = 1/8 dans le contexte d'une course. Le premier coureur faisait 7/8 de tour de piste alors que le deuxième coureur faisait 3/4 de tour de piste. Quelle était l'avance du premier coureur ? (1/8 de la piste).
Fiches d'exercices sur la soustraction de fractions mixtes

En mélangeant les signes sur les opérations avec les feuilles de travail sur les fractions, les élèves sont plus attentifs à ce qu'ils font et peuvent tester leurs compétences dans plus d'une opération.
Addition et soustraction de fractions

Fiches d'exercices sur la priorité des opérations sur les fractions
Comme pour les autres fiches de priorité des opérations, les fiches de priorité des fractions nécessitent des connaissances préalables. Si vos étudiants ont du mal à répondre à ces questions, cela tient probablement plus à leur capacité à travailler avec des fractions qu'aux questions elles-mêmes. Observez attentivement et essayez de déterminer exactement les connaissances préalables qui manquent, puis passez un peu de temps à revoir ces concepts/compétences avant de poursuivre. Sinon, les fiches de travail ci-dessous devraient donner des réponses assez simples et ne devraient pas entraîner une trop grande perte de cheveux.
La priorité des opérations sur les fractions

