Fiches d'Exercices sur les Nombres Entiers Naturels

Bienvenue à la page Nombres Entiers de MathsLibres.com! Vous y vivrez probablement quelques expériences négatives, mais dans le monde des nombres entiers ceci n'est point un malheur!

Le contenu de cette page traite sur l'ensemble des nombres entiers relatifs, mais il porte une attention spéciale à l'introduction des entiers négatifs. Il n'est pas rare, dans notre vie de tout les jours, de tomber sur des nombres négatifs. Si vous avez déjà passé du temps au Canada en Janvier, vous avez sûrement, durant votre séjour, vécu de première main l'expérience d'un nombre négatif. à la banque, vous avez peut-être auparavant eu le malaise de souffrir des charges d'intérêt abusives pour le simple fait d'avoir laisser la balance de votre compte tomber sous zéro. Lorsqu'on part en plongée sous-marine, il faut être prêt à s'immerger dans le territoire des nombres négatifs. Ceci dit, même si on ne compte pas visiter le Canada, devenir comptant ou être plongeur sous-marin professionnel, il y plusieurs autres raisons qui motivent l'acquisition d'une bonne connaissance des nombre négatifs. L'une des plus importantes entre elles étant que plusieurs sujets de mathématiques au secondaire requièrent un bon sens de ces nombres.

Pour supporter vos élèves dans leur conquête académique, nous avons inclus, sur cette page, quelques centaines de fiches d'exercices sur les nombres entiers traitant la comparison, classification en ordre, l'addition, soustraction, multiplication et la division, ainsi que toute une section dédiée aux opérations mixtes. Nous vous recommandons aussi, si vous êtes enseignants, de vous procurer d'une grande droite numérique pour le mur de votre classe ou d'avoir en main quelques une de nos pages de droites numériques imprimables. Vous pouvez aussi les projeté sur votre tableau blanc ou en faire un transparent. Pour les éducateurs à domicile ou les enseignants qui n'ont que quelques étudiants, les fiches imprimées devraient suffirent. Nous recommandons aussi l'utilisation des jetons à deux couleurs. Veuillez voir les sections « Addition » et « Soustraction » ci-dessous pour plus d'informations sur ces jetons.

Fiches d'Exercices sur les Nombres Entiers Naturels le Plus Populaires cette Semaine

Addition de Nombres Entiers de (-9) à (+9) (Parenthèses sur les Nombres Négatifs) (**18 vues cette semaine**)

Représentation sur une Droite Numérique de Nombres Entiers Naturels de -20 à 20 (**6 vues cette semaine**)

Toutes les Opérations avec des Nombres Entiers de -15 à 15 (Sans les Parenthèses) (**6 vues cette semaine**)

Soustraction de Nombres Entiers de (-9) à 9 (Parenthèses sur les Nombres Négatifs) (**5 vues cette semaine**)

Addition de Nombres Entiers de (-99) à (+99) (Avec des Parenthèses) (**5 vues cette semaine**)

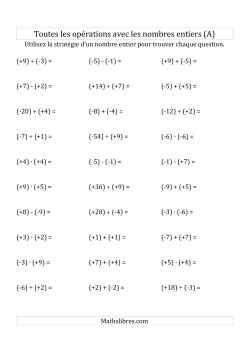
Ressources

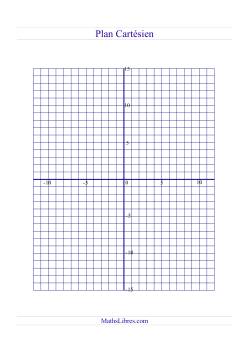
Ces Ressources comprennent le plan cartésien et la droite numérique.

Plan Cartésien & Droite Numérique

Plan Cartésien (x,y: -15 à 15)

Représentation sur une droite numérique de nombres entiers naturels

Représentation sur une Droite Numérique de Nombres Entiers Naturels de -10 à 10 Représentation sur une Droite Numérique de Nombres Entiers Naturels de -15 à 15 Représentation sur une Droite Numérique de Nombres Entiers Naturels de -20 à 20 Représentation sur une Droite Numérique de Nombres Entiers Naturels de -25 à 25 Classification en Ordre sur Une Droite Numérique (ANCIENS) Droite Numérique - Nombres Entiers (ANCIENS)

Comparaison et Ordre des Nombres Entiers Naturels

Fiches d'exercices sur la comparison des nombres entiers pour apprendre l'ordinalité de nombres entiers.

Fiches d'exercices sur la comparaison de nombres entiers

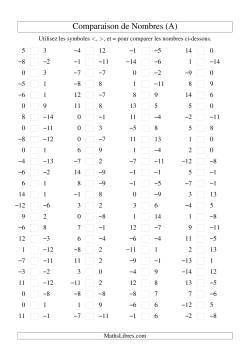
Comparaison - Nombres Entiers Positifs/Négatifs (-15 à +15) (100 par page) Comparaison - Nombres Entiers Positifs/Négatifs (-15 à +15) (60 par page) Comparaison - Nombres Entiers Négatifs (-15 à -1) (100 par page) Comparaison - Nombres Entiers Négatifs (-15 à -1) (60 par page)

Ordre de Nombres Entiers

La comparaison de nombres entiers permet de situer ces nombres les uns par rapport aux autres. On peut alors les placer en ordre croissant ou en ordre décroissant.

Placer en Ordre des Nombres Entiers de -9 à 9 Placer en Ordre des Nombres Entiers de -20 à 20 Placer en Ordre des Nombres Entiers de -50 à 50 Placer en Ordre des Nombres Entiers de -99 à 99 Placer en Ordre des Nombres Entiers de -999 à 999 Placer en Ordre des Nombres Entiers Négatifs de -9 à -1 Placer en Ordre des Nombres Entiers Négatifs de -99 à -10 Placer en Ordre des Nombres Entiers Négatifs de -999 à -100

Addition de Nombres Entiers

Fiches d'exercices sur l'addition des nombres entiers en différentes gammes comprennant une variété d'options sur l'utilisation de parenthèses.

Avez-vous déjà entendu parlé des jetons à deux couleurs et de comment ils peuvent rendre plus faciles et plus amusantes l'étude ainsi que l'enseignement des nombres négatifs? Certes, vous pourriez simplement apprendre à vos élèves les règles de ++, +−, −+, et −−, mais cette méthode manque un peu de coloration. D'habitude, ces jetons sont fait en plastic coloré jaune d'un bord et rouge de l'autre. Bien sûr, il se peut que vous en trouviez de différente teinture, alors vous aurez peut-être en lisant à remplacer nos couleurs par les vôtres.

L'addition avec deux couleur est étonnamment simple. Vous commencez par modelé le premier nombre de l'opération avec une pile de jetons tous tournés du bon bord, vous représentez ensuite le deuxième nombre de la même façon. Ceci fait, vous mélangez les deux piles, ensuite vous n'avez qu'À retirer les zéros (s'il y ont lieu), et voilÀ! vous avez votre réponse. Comme nous pouvons voir quelques regards confus dans la foule, nous allons expliquer un peu plus en détail.

Par le « bon bord » nous voulons dire le bord rouge pour les nombres négatifs et le jaune pour les positifs. Par exemple, pour modeler le nombre -5 vous avez besoin d'une pile de cinq jetons rouges, tandis que 7 requiert sept jetons jaunes. Ensuite, lorsque vous mélangez les piles, faites bien attention de ne pas retourner de jetons. En vérité, vous n'avez qu'À doucement rapprocher les deux piles jusqu'à ce qu'ils se combinent en une seule. Pour obtenir un zéro, vous avez besoin d'une paire de jetons des deux différentes couleurs, un rouge et un jaune, alors aussitôt que votre pile est formée il faut retirer le plus de paires jaune-rouge possibles. Cette étape ne change pas le problème, car lorsqu'on ajoute -1 à 1 on obtient zéro (ceci s'appelle le principe de zéro de toute chose), et si vous soustrayez zéro d'un nombre, il reste invarié. En enlevant toutes les paires zéro vous obtiendrez toujours une pile qui ne contient pas plus qu'une couleur de jetons et, par conséquent, vous aurez obtenu la solution à votre problème.

Addition de nombres entiers avec des parenthèses sur tous les nombres entiers

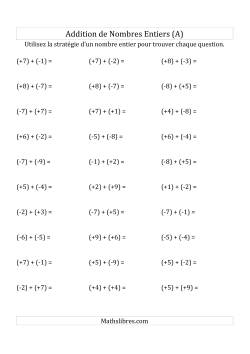
Addition de Nombres Entiers de (-9) à (+9) (Avec des Parenthèses) Addition de Nombres Entiers de (-15) à (+15) (Avec des Parenthèses) Addition de Nombres Entiers de (-25) à (+25) (Avec des Parenthèses) Addition de Nombres Entiers de (-50) à (+50) (Avec des Parenthèses) Addition de Nombres Entiers de (-99) à (+99) (Avec des Parenthèses)

Addition de nombres entiers avec des parenthèses sur les nombres négatifs seulement

Addition de Nombres Entiers de (-9) à 9 (Parenthèses sur les Nombres Négatifs) Addition de Nombres Entiers de (-15) à 15 (Parenthèses sur les Nombres Négatifs) Addition de Nombres Entiers de (-25) à 25 (Parenthèses sur les Nombres Négatifs) Addition de Nombres Entiers de (-50) à 50 (Parenthèses sur les Nombres Négatifs) Addition de Nombres Entiers de (-99) à 99 (Parenthèses sur les Nombres Négatifs)

Soustraction de Nombres Entiers

Fiches d'exercices sur la soustraction des nombres entiers en différentes gammes comprennant une variété d'options sur l'utilisation de parenthèses.

La soustraction des nombres entiers à l'aide des jetons à deux couleurs s'effectuent un peu différemment de l'addition. Pour effectuer une soustraction avec ces jetons, commencez par modeler le premier nombre (le diminuende) avec les jetons. Par la suite, enlevez assez de jetons de la pile pour pouvoir équivaler la valeur du deuxième nombre (le diminuteur), et vous aurez votre réponse. Malheureusement, ceci ne représente pas exactement la façon dont il faut procéder. Si la pile de départ contient déjà assez de jetons à retirer de la bonne couleur, cette méthode fonctionne parfaitement, mais qu'est-ce qu'il y arrive si ceci n'est pas le cas? Par exemple, pour effectuer 5 − (−5) vous commenceriez avec une pile de cinq jetons jaune et vous auriez à enlever cinq jetons rouges, mais la pile ne contient pas de jetons rouges. Dieu merci, nous avons le principe de zéro. L'addition ou la soustraction de zéro (un jeton rouge et un jeton jaune) n'affecte pas le nombre du début, alors nous pouvons ajouter autant de zéros à la pile que nous le souhaitons sans changer notre question. Nous n'avons donc qu'À ajouter autant de zéros que de jetons qu'il nous reste à soustraire. Dans notre exemple 5 − (− 5), vous ajouteriez 5 zéros pour que vous puissiez retirer les cinq jetons rouges. à ce point lÀ il vous resterait 10 jetons jaunes (ou +10) ce qui vous donnerait votre réponse.

Soustraction de nombres entiers avec des parenthèses sur tous les nombres entiers

Soustraction de Nombres Entiers de (-9) à (+9) (Avec des Parenthèses) Soustraction de Nombres Entiers de (-15) à (+15) (Avec des Parenthèses) Soustraction de Nombres Entiers de (-25) à (+25) (Avec des Parenthèses) Soustraction de Nombres Entiers de (-50) à (+50) (Avec des Parenthèses) Soustraction de Nombres Entiers de (-99) à (+99) (Avec des Parenthèses)

Soustraction de nombres entiers avec des parenthèses sur les nombres négatifs seulement

Soustraction de Nombres Entiers de (-9) à 9 (Parenthèses sur les Nombres Négatifs) Soustraction de Nombres Entiers de (-15) à 15 (Parenthèses sur les Nombres Négatifs) Soustraction de Nombres Entiers de (-25) à 25 (Parenthèses sur les Nombres Négatifs) Soustraction de Nombres Entiers de (-50) à 50 (Parenthèses sur les Nombres Négatifs) Soustraction de Nombres Entiers de (-99) à 99 (Parenthèses sur les Nombres Négatifs)

Soustraction de nombres entiers avec aucunes parenthèses

Soustraction de Nombres Entiers de -9 à 9 (Sans les Parenthèses) Soustraction de Nombres Entiers de -15 à 15 (Sans les Parenthèses) Soustraction de Nombres Entiers de -25 à 25 (Sans les Parenthèses) Soustraction de Nombres Entiers de -50 à 50 (Sans les Parenthèses) Soustraction de Nombres Entiers de -99 à 99 (Sans les Parenthèses)

Soustraction de nombres entiers arrangés verticalement

Soustraction de Nombres Entiers à 3 Chiffres (Arrangés Verticallement) Soustraction d'un Entier Positif à 3 Chiffres par un Entier Positif (Arrangés Verticalement) Soustraction d'un Entier Positf à 3 Chiffres par un Entier Négatif (Arrangés Verticalement) Soustraction d'un Entier Négatif à 3 Chiffres par un Entier Positf (Arrangés Verticalement) Soustraction d'un Entier Négatif à 3 Chiffres par un Entier Négatif (Arrangés Verticalement)

Addition et Soustraction Mixtes de Nombres Entiers

Fiches d'exercices sur l'addition et la soustraction mixtes des nombres entiers en différentes gammes comprennant une variété d'options sur l'utilisation de parenthèses.

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -5 à +5

Parenthèses autour tout entiers (Variations (-5) à (+5)) (75 par page) Parenthèses autour tout entiers (Variations (-5) à (+5)) (45 par page)

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -9 à +9

Parenthèses autour tout entiers (Variations (-9) à (+9)) (75 par page) Parenthèses autour tout entiers (Variations (-9) à (+9)) (45 par page)

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -25 à +25

Parenthèses autour tout entiers (Variations (-25) à (+25)) (75 par page) Parenthèses autour tout entiers (Variations (-25) à (+25)) (45 par page)

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -75 à +75

Parenthèses autour tout entiers (Variations (-50) à (+50)) (75 par page) Parenthèses autour tout entiers (Variations (-50) à (+50)) (45 par page)

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -10 à +10

Parenthèses autour négatifs seulement (Variations (-10) à 10) (75 par page) Parenthèses autour négatifs seulement (Variations (-10) à 10) (45 par page)

Fiches d'exercices sur l'addition et la soustraction mixtes de nombres entiers variant de -99 à +99

Parenthèses autour négatifs seulement (Variations (-99) à 99) (75 par page) Parenthèses autour négatifs seulement (Variations (-99) à 99) (45 par page)

Multiplication de Nombres Entiers

Fiches d'exercices sur la multiplication de nombres entiers en différentes gammes et incluant des fiches d'exercices qui mettent l'accent sur des types particuliers d'opérations sur les nombres entiers.

Fiches d'exercices sur lamultiplication mixte de nombres entiers variant de -12 à +12

Mixtes avec variations de (-12) à 12 (75 par page) Mixtes avec variations de (-12) à 12 (45 par page)

Fiches d'exercices sur lamultiplication mixte de nombres entiers variant de -20 à +20

Mixtes avec variations de (-20) à 20 (75 par page) Mixtes avec variations de (-20) à 20 (45 par page)

Fiches d'exercices sur lamultiplication mixte de nombres entiers variant de -50 à +50

Mixtes avec variations de (-50) à 50 (75 par page) Mixtes avec variations de (-50) à 50 (45 par page)

Fiches d'exercices sur lamultiplication de nombres entiers (positif & négatif mixtes)

Positif × Négatif (75 par page) Positif × Négatif (45 par page) Négatif × Positif (75 par page) Négatif × Positif (45 par page) Négatif × Négatif (75 par page) Négatif × Négatif (45 par page)

Division de Nombres Entiers

Fiches d'exercices sur la division de nombres entiers en différentes gammes et incluant des fiches d'exercices qui mettent l'accent sur des types particuliers d'opérations sur les nombres entiers.

Fiches d'exercices sur ladivision mixte de nombres entiers variant de -12 à +12