Bienvenue à la page Algèbre de MathsLibres.com, où les inconnues sont toujours les bienvenues. Sur cette page vous allez trouver des opérations sur les relations inverses, termes manquants et variables, expressions linéaires et équations, diverses expressions quadratiques et système d'inéquation incluant des graphiques.
La plupart des sections ci-dessous sont destinées aux élèves du début secondaire, mais nous avons aussi inclu quelques sujets plus avancés pour les étudiants plus aînés. La page commence tout d'abord avec une section sur les relations inverses et le remplacement de termes manquants et variables qui est destinée aux élèves plus jeunes. Ensuite, pour initier vos élèves au language de l'algèbre, nous avons placé des exercices de traduction de phrases écrites en formules algébriques. Le restant de la page traite sur une variété de thèmes qui ve retrouverez d'habitude dans les modules scolaires de l'algèbre à savoir les expressions linéaires & équations et les Expressions Quadratiques & Équations. Gardez en tête que lorsque vous enseigniez l'algèbre à vos élèves, vous êtes en train de former les futures scientifiques, ingénieurs et génies financiers du monde entier.
L'étude de l'algèbre devient beaucoup plus intéressante lorsqu'on y attache des interprétations concrètes. Il est plus amusant de résoudre des équations linéaires à l'aide d'une balance à deux fléaux, de quelques sacs mystère et d'une montagne de petits caramels. Plusieurs enseignants aiment aussi se servir des tuiles d'algèbre pour démontrer certains concepts. Enfin, il n'y a rien de plus génial qu'une paire d'axes de coordonnées lorsqu'on cherche à résoudre un système d'équations linéaires.
Fiches d'Exercices sur l'Algèbre le Plus Populaires cette Semaine




Relations Inverses
Ces fiches d'exercices sur les relations inverses couvrent une compétence de pré-algèbre destinée à aider les élèves à comprendre la relation entre la multiplication et de division, ainsi que celle entre l'addition et la soustraction.
Fiches d'exercices sur les relations inverses avec une espace vide

Fiches d'exercices sur les relations inverses avec deux espaces vides
Termes Manquants et Variables
Les fiches de cette section ont pour but d'introduire le concept d'une variable. Dans une équation, l'utilisation d'une variable indique la présence d'une valeur ou d'une quantité inconnue. Souvent, le simple fait d'utiliser une lettre de l'alphabet pour représenter cette quantité laisse les élèves débutants perdus et bafouillés. Nous recommendons donc, tout d'abord, de commencer avec les fiches « Termes Manquants » qui utilisent des espaces blancs à la place des variables, et de par la suite introduire les variables tout en leur faisant le lien avec le concept des termes manquants.
Fiches d'exercices sur l'algèbre avec des termes manquants comme inconnues

Fiches d'exercices sur l'algèbre avec des variables comme inconnues

Les Propriétés des Exposants
Comme le titre l'indique, ces fiches d'exercices incluent seulement des questions de propriétés des exposants de base. Chaque question ne contient que deux exposants à traiter; nous avons mis de coté des termes un peu plus complexes qu'un élève plus avancé aurait besoin de travailler sur. Par exemple, 42 nous donne (22)2 = 22, mais ces fiches d'exercices laissent la réponse juste comme 42.
Pratiques avec les propriétés des exposants de base
Expressions Linéaires & Équations
Ces fiches d'exercices sur les équations linéaires contiennent la traduction, le réaménagement, la simplification, l'évaluation et la résolution des systèmes d'équations linéaires.
Réécrire une équation linéaire

Équations linéaires à partir d'une pente, point d'intersection et points
Fiches d'exercices sur le réaménagement d'une formule

Fiches d'exercices sur la simplification d'expressions algébriques
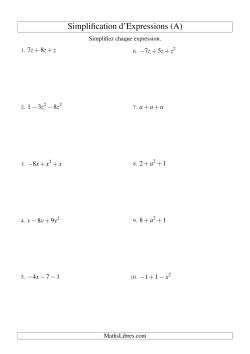
Fiches d'exercices sur la évaluation d'expressions algébriques

Fiches d'exercices sur la résolution d'équations linéaires sans des termes "b"

Vous avez peut-être été intrigués par notre commentaire plus haut à propos des caramels qui aident à résoudre les équations linéaires. Voici comment ce peut se faire. Idéalement, vous voudriez avoir quelques sacs opaques sans masse, mais comme ceci n'est pas tout à fait possible (vous aurez de la difficulté à trouvez des sacs sans masse), nous nous retrouvons par hasard avec une condition qui aidera les élèves à encore mieux comprendre les équations linéaires. Sachez que tout sac que vous utiliserez sur un côté de la balance devra être équilibré de l'autre côté par un autre sac.
Il sera plus simple d'illustrer cette méthode avec un exemple. Prenons l'équation 3x + 3 = 14. Içi, le x est la variable inconnue qui coincide avec le montant de caramels qui se trouve dans le sac mystère. Le coefficient 3 du terme 3x signifie qu'il nous faudra 3 sacs de x caramels. Notez qu'il est préférable de remplir les sacs mystères hors de la vue de vos élèves pour que le montant de leur contenu, la valeur de x, soit vraiment un mystère.
Sur un des fléaux de la balance, placez les 3 sacs de x caramels. Ajoutez-y 2 autre caramels libres pour représenter le + 2 de l'équation. Sur l'autre fléaux, placez 14 caramels et les trois sac qui seront nécessaires pour équilibrer la balance. Et maintenant, on passe à la partie amusante... si l'élève enlève les deux caramels libres dans le premier fléaux, la balance devient désiquilibrée, alors il est forcé à enlever deux caramels de l'autre côté pour pouvoir maintenir l'équilibre. à ce point ci, l'élève commencera peut-être à manger les caramels dégagés. Le but de cette étape est d'isoler les sacs mystères sur un bord de la balance tout en maintenant l'équilibre.
La dernière étape est de diviser les caramels libres tout aménagés sur un bord de l'équation dans des groupes égaux dont le nombre équivaut celui des sacs mystères qui se trouvent de l'autre bord de l'équation. Ceci donnera généralement une bonne idée du nombre de caramels qui se trouvent dans les sacs mystères. Si ce n'est pas le cas, nous recommandons de manger quelques caramels et d'ensuite réessayer. D'ailleurs, vous avez sûrement remarqué qu'il existe des équations linéaires pour lesquelles ce jeu ne fonctionnera pas (il est vachement difficile de mettre un nombre négatif de caramels dans un sac). Laissez le temps à vos élèves d'expérimenter avec leurs propres équations et de s'en rendre compte eux aussi de ce fait.
Fiches d'exercices sur la résolution d'équations linéaires incluant la multiplication et des termes "b"

Fiches d'exercices sur la résolution d'équations linéaires incluant la division et des termes "b"
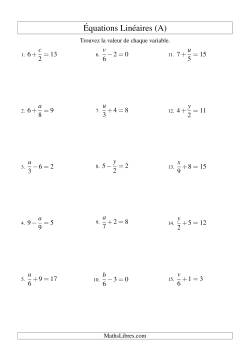
Fiches d'exercices sur la résolution d'équations linéaires mixtes

Fiches d'exercices sur les systèmes d'équations linéaires (ou système linéaire)

Expressions Quadratiques & Équations
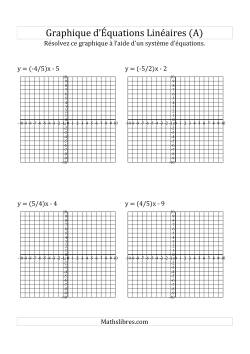
Avez-vous besoin de quelques pratiques graphiques des équations linéaires? Ne cherchez pas plus loin que sur cette section.
Représentation graphique d’équations linéaires
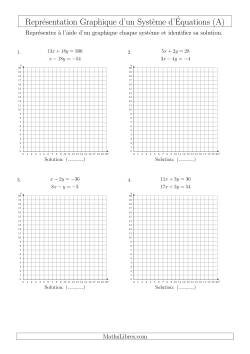
Représentation graphique d'un système d'équations
Fiches d'exercices sur la multiplication de facteurs d'expressions quadratiques

Fiches d'exercices sur la factorisation d'expressions quadratiques

Les fiches d'Exercices sur la Factorisation d'Expressions Quadratiques ci-dessous fournissent beaucoup de questions pratiques aux élèves afin d'affiner leurs stratégies de factorisation. Si vous voulez plutôt des fiches d'exercices avec des équations quadratiques, veuillez consulter la section suivante. Ces fiches d'exercices viennent dans une variété de niveaux avec les plus faciles au début. Les coefficients «a» mentionnés ci-dessous sont les coefficients du terme x², comme dans l'expression générale quadratique suivante: ax² + bx + c.
Fiches d'exercices sur les équations quadratiques qui égalent à Zéro (ex: ax² + bx + c = 0)

Ces fiches d'exercices incluent une pléthore de questions pratiques avec leurs réponses. Dans la première section, les fiches d'exercices incluent des questions où les expressions quadratiques égalent à 0. Cela rend le processus similaire à la factorisation d'expressions quadratiques, avec une étape supplémentaire de trouver les valeurs de x, lorsque l'expression est égale à 0. Dans la deuxième section, les expressions sont généralement égales à un nombre autre que x, donc il y a une étape supplémentaire au début pour faire l'expression quadratique soit égale à zéro.
Fiches d'exercices sur les équations quadratiques qui égalent à nombre (ex: ax² + bx + c = d)

Factorisation d'Expressions Sans Utiliser la Formule Quadratique
Des fiches d'exercices sur la factorisation d'expressions sans utiliser la formule quadratique avec différents niveaux de complexité.
Fiches d'exercices sur les expressions qui n'incluent aucun terme avec une racine carrée

Fiches d'exercices sur les expressions qui incluent toujours un terme avec une racine carrée

Fiches d'exercices sur les expressions qui incluent de fois un terme avec une racine carrée

Multiplication d'Expressions Quadratiques
Des fiches d'exercices sur la multiplication d'expressions quadratiques. Lors de la multiplication un monôme par un polynôme, nous appliquons la distributivité de la multiplication sur l'addition et le monôme multiplie alors chacun des termes du polynôme.
De même lors de la multiplication d'un polynôme par un autre polynôme, chacun des termes du premier polynôme doit multiplier chacun des termes du deuxième polynôme.
Multiplication de polynômes qui ont deux facteurs

Multiplication de polynômes qui ont trois facteurs
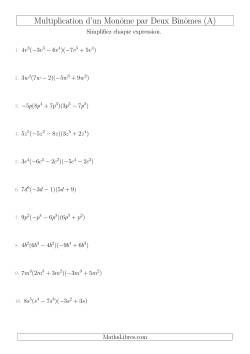
Systèmes d’Inéquations Incluant des Graphiques
Fiches d'exercices sur les systèmes d’inéquations incluant l'écriture des systèmes et la repésenation graphique d'inéquations sur une droite graduée.
Écrire des systèmes d'inéquations qui correspondent aux représenations graphiques

Représentation graphique d'une inéquation sur une droite graduée


